解方程组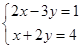
先化简,再求值:(2x+1)(x-2)-(2-x)2, 其中x=-2.
如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限内.
(1)如图1,写出点B的坐标();
(2)如图2,若过点C的直线CD交线段AB于点D,且把长方形OABC的周长分为3:1两部分,求点D的坐标;
(3)如图3,将(2)中的线段CD向下平移2个单位,得到C/D/,试计算四边形OAD/C/的面积.
长沙市某公园的门票价格如下表所示:
某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲、乙两班分别有多少人?
把一副三角板的直角顶点O重叠在一起,
(1)如图(1),当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?