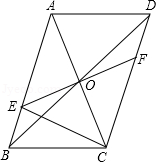
如图,在数轴上点A、B、C表示的数分别为-2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)则AB= , BC= ,AC= ;

(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动。请问:BC-AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;

(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:当运动时间t在0~1秒之间时, AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.

已知, 为直角三角形, ,点 是射线 上一点(点 不与点 、 重合),线段 绕点 顺时针旋转 得到线段 ,连接 交射线 于点 .
(1)如图①,当 ,点 在线段 上时,线段 、 的数量关系是 ;
(2)如图②,当 ,点 在线段 的延长线时,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由.
(3)如图③,若
,点
在线段
的延长线上,
,
,求
的面积.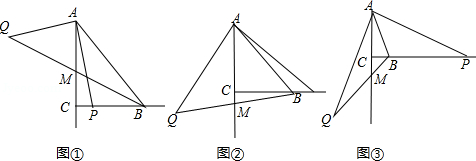
如图,某巡逻艇计划以40海里 时的速度从 处向正东方向的 处航行,出发1.5小时到达 处时,突然接到 处的求救信号,于是巡逻艇立刻以60海里 时的速度向北偏东 方向的 处航行,到达 处后,测得 处位于 处的南偏西 方向,解救后巡逻艇又沿南偏东 方向航行到 处.
(1)求巡逻艇从 处到 处用的时间.
(2)求巡逻艇实际比原计划多航行了多少海里?(结果精确到1海里).
(参考数据:

某公司研发了一款成本为60元的保温饭盒,投放市场进行试销售,按物价部门规定,其销售单价不低于成本,但销售利润不高于 ,市场调研发现,保温饭盒每天的销售数量 (个 与销售单价 (元 满足一次函数关系;当销售单价为70元时,销售数量为160个;当销售单价为80元时,销售数量为140个(利润率
(1)求 与 之间的函数关系式;
(2)当销售单价定为多少元时,公司每天获得利润最大,最大利润为多少元?
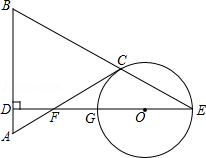
如图, 中, ,点 是线段 延长线上一点, ,垂足为 , 交线段 于点 ,点 在线段 上, 经过 、 两点,交 于点 .
(1)求证: 是 的切线;
(2)若 , , ,求 的半径.
如图, 的对角线 、 相交于点 , 过点 且与 、 分别相交于点 、 ,连接 .
(1)求证: ;
(2)若 , 的周长是10,求 的周长.