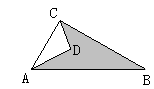
(本题8分) 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1.
(1)求证 :∠BPQ=60°(提示:利用三角形全等、外角的性质)
(2)求BE的长.
如图所示,在△ABC中:
(1)画出BC边上的高AD和中线AE.
(2)若∠B=30°,∠ACB=130°,求∠BAD和∠CAD的度数.
已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M。请探究:
(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论。
(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;
(3)如图(3),当点E在CA的延长线上,点D在线段AB上(点D不与A,B重合),DE所在直线与直线BC交于点M,若CE=2BD,请直接写出线段MD与线段ME的数量关系。
如图,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB = 8cm,BC =" 10" cm,求EC的长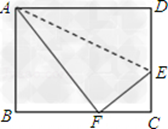
已知,如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点。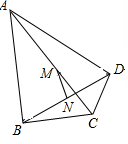
求证:①BM=DM②MN⊥BD.
已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分的面积.