已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,。经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图①,连接DE,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,连接AD,点F是抛物线上A、C之间的一点,直线BF交AD于点P,连接PE, 试探索BP+PE是否存在最小值?若存在,求出这个最小值,并直接写出此时点F的坐标;若不存在,请说明理由.
李明骑自行车去上学途中,经过先上坡后下坡的一条路段,在这段路上所走的路程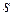 (米)与时间
(米)与时间 (分钟)之间的函数关系如图所示.根据图象,解答下列问题:
(分钟)之间的函数关系如图所示.根据图象,解答下列问题: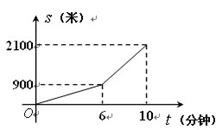
(1)求李明上坡时所走的路程 (米)与时间t(分钟)之间的函数关系式和下坡时所走的路程
(米)与时间t(分钟)之间的函数关系式和下坡时所走的路程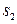 (米)与时间t(分钟)之间的函数关系式;
(米)与时间t(分钟)之间的函数关系式;
(2)若李明放学后按原路返回,且往返过程中,上坡的速度相同,下坡的速度也相同,问李明返回时走这段路所用的时间为多少分钟?
河池市近年来大力发展旅游业,吸引了众多外地游客前来观光旅游,某旅行社对2009年“十·一”国庆期间接待的外地游客作了抽样调查.河池的首选旅游线路(五大黄金旅游线路)的调查结果如下图表:(如下图)
(1)此次共抽样调查了人;
(2)请将以上图表补充完整;
(3)该旅行社预计五大黄金旅游线路今年“十·一”国庆期间接待外地游客约20000人,请你估计外地游客首选三姐故乡游的人数约有人.
(满分8分,每小题4分)
(1)计算: (2)解方程:
(2)解方程:
(满分13分)如图11,在平面直角坐标系中,直线 与
与 轴、
轴、 轴分别交于点B、C ;抛物线
轴分别交于点B、C ;抛物线 经过B、C两点,并与
经过B、C两点,并与 轴交于另一点A.
轴交于另一点A.
(1)求该抛物线所对应的函数关系式;
(2)设 是(1)所得抛物线上的一个动点,过点P作直线
是(1)所得抛物线上的一个动点,过点P作直线 轴于点M,交直线BC于点N .
轴于点M,交直线BC于点N .
① 若点P在第一象限内.试问:线段PN的长度是否存在最大值 ?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
② 求以BC为底边的等腰△BPC的面积.
(满分11分)
如图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H.
(1)证明:△ABG  △ADE ;
△ADE ;
(2)试猜想 BHD的度数,并说明理由;
BHD的度数,并说明理由;
(3)将图中正方形ABCD绕点A逆时针旋转(0°< BAE <180°),设△ABE的面积为
BAE <180°),设△ABE的面积为 ,△ADG的面积为
,△ADG的面积为 ,判断
,判断 与
与 的大小关系,并给予证明.
的大小关系,并给予证明.