已知定义域为R的函数f(x)在区间(4,+∞)上为减函数,且函数y=f(x+4)
为偶函数,则()
| A.f(2)>f(3) | B.f(2)>f(5) | C.f(3)>f(5) | D.f(3)>f(6) |
下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是()
| A.y=x3 | B.y=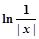 |
C.y=2|x| | D.y=cosx |
函数y= 的值域是()
的值域是()
| A.[0,+∞) | B.(0,4] | C.[0,4) | D.(0,4) |
已知直线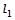 :x+ay+6=0和
:x+ay+6=0和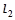 :(a-2)x+3y+2a=0,则
:(a-2)x+3y+2a=0,则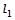 ∥
∥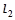 的充要条件是a=()
的充要条件是a=()
| A.3 | B.1 | C.-1 | D.3或-1 |
对命题“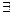 x0∈R,x02-2x0+4≤0”的否定正确的是()
x0∈R,x02-2x0+4≤0”的否定正确的是()
A.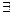 x0∈R,x02-2x0+4>0 x0∈R,x02-2x0+4>0 |
B.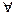 x∈R,x2-2x+4≤0 x∈R,x2-2x+4≤0 |
C.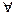 x∈R,x2-2x+4>0 x∈R,x2-2x+4>0 |
D.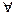 x∈R,x2-2x+4≥0 x∈R,x2-2x+4≥0 |