(·黑龙江哈尔滨)小明家、公交车站、学校在一条笔直的公路旁(小明家到这条公路的距离忽略不计)。一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示。已知小明从家出发7分钟时与家的距离为1200米,从上车到他到达学校共用10分钟。下列说法:
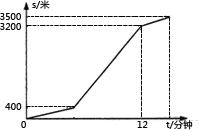
①小明从家出发5分钟时乘上公交车
②公交车的速度为400米/分钟
③小明下公交车后跑向学校的速度为100米/分钟
④小明上课没有有迟到。
其中正确的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知某二次函数的图象如图所示,则这个二次函数的解析式为()
| A.y=﹣3(x﹣1)2+3 | B.y=3(x﹣1)2+3 |
| C.y=﹣3(x+1)2+3 | D.y=3(x+1)2+3 |
如图,抛物线的顶点P的坐标是(1,﹣3),则此抛物线对应的二次函数有()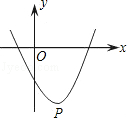
| A.最大值1 | B.最小值﹣3 | C.最大值﹣3 | D.最小值1 |
形状、开口方向与抛物线y=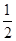 x2相同,但是顶点为(﹣2,0)的抛物线解析式为()
x2相同,但是顶点为(﹣2,0)的抛物线解析式为()
A.y=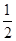 (x﹣2)2 (x﹣2)2 |
B.y=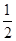 (x+2)2 (x+2)2 |
C.y=﹣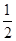 (x﹣2)2 (x﹣2)2 |
D.y=﹣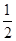 (x+2)2 (x+2)2 |
如果将二次函数y=3x2的图象向上平移5个单位,得到新的图象的二次函数表达式是()
| A.y=3x2﹣5 | B.y=3(x﹣5)2 | C.y=3x2+5 | D.y=3(x+5)2﹣5 |
在一次足球比赛中,守门员用脚踢出去的球的高度h随时间t的变化而变化,可以近似地表示这一过程的图象是()
A. |
B. |
C. |
D. |