（·黑龙江省黑河市、齐齐哈尔市、大兴安岭）【6分】如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A、C分别在x轴、y轴的正半轴，抛物线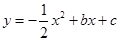
经过B、C两点，点D为抛物线的顶点，连接AC、BD、CD．
（1）求此抛物线的解析式．
（2）求此抛物线顶点D的坐标和四边形ABCD的面积．
图为一位旅行者在早晨8时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
（1）在这个变化过程中，自变量是，因变量是。
（2）9时，10时，12时所走的路程分别是多少？
（3）他休息了多长时间？
（4）他从休息后直至到达目的地这段时间的平均速度是多少？
已知：如图，AE=AC，BE=DC，求证：△ABC≌△ADE.
根据题意，将证明过程的理由填写在后面的括号内。
已知：如图,AB∥CD，AD∥BC. 求证：∠A＝∠C .
证明：∵AB∥CD（_________）
∴∠B+∠C=180°（）
∵AD∥BC（已知）
∴∠A+∠B=180°（）
∴∠A＝∠C . ()
如果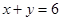
，
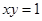，求
的值。
化简求值：
，其中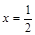
，
.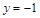