（·黑龙江绥化）现有甲、乙两个容器，分别装有进水管和出水管 ，两容器的进出水速度不变，先打开乙容器的进水管，2分钟时再打开甲容器的进水管 ，又过2分钟关闭甲容器的进水管，再过4分钟同时打开甲容器的进、出水管．直到12分钟时，同时关闭两容器的进出水管,打开和关闭水管的时间忽略不计。容器中的水量y（升）与乙容器注水时间x之间的关系如图所示:
（1）求甲容器的进、出水速度．
（2）甲容器进、出水管都关闭后，是否存在两容器的水量相等。若存在，求出此时的时间．
（3）若使两容器第12分钟时水量相等，则乙容器6分钟后进水速度应变为多少？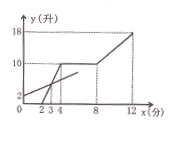
如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．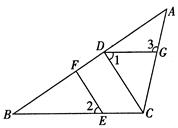
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2，且∠3=115°，求∠ACB的度数．
反比例函数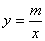
的图象与一次函数y=ax+b的图象交于A（1，3）和B（n,-1）两点.
（1）求这两个函数的解析式，并画出草图;
（2）根据图象回答当x取何值时，反比例函数的值大于一次函数的值;
（3）连接OA、OB, 求⊿AOB的面积.
比邻而居的蜗牛神和蚂蚁王相约，第二天上午8时结伴出发，到相距16米的银杏树下参加探讨环境问题的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训，于是在第二天早上6：40给蚂蚁王留下一张纸条后独自先行，蚂蚁王按既定时间出发，结果它们同时到达.已知蚂蚁王的速度是蜗牛神的3倍，求它们各自的速度.
如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形（涂上阴影）．
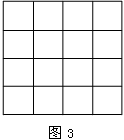
⑴在图1中，画一个直角三角形，使它的三边长都是有理数；
⑵在图2、图3中，分别画一个直角三角形，使它的三边长都是无理数(两个三角形不全等)
在某一平地上，有一棵高6米的大树，一棵高3米的小树，两树之间相距4米。今一只小鸟在其中一棵树的树梢上要飞到另一棵树的树梢上，问它飞行的最短距离是多少？