(·辽宁营口)如图1,一条抛物线与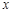 轴交于A,B两点(点A在点B的左侧),与
轴交于A,B两点(点A在点B的左侧),与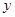 轴交于点C,且当x=-1和x=3时,
轴交于点C,且当x=-1和x=3时,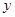 的值相等.直线
的值相等.直线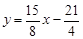 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为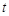 秒.
秒.
①若使△BPQ为直角三角形,请求出所有符合条件的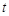 值;
值;
②求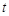 为何值时,四边形ACQ P的面积有最小值,最小值是多少?
为何值时,四边形ACQ P的面积有最小值,最小值是多少?
(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥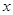 轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿
轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿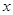 轴向左平移
轴向左平移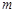 个单位长度(
个单位长度(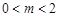 ),将平移后的三角形与△ODM重叠部分的面积记为
),将平移后的三角形与△ODM重叠部分的面积记为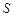 ,求
,求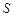 与
与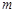 的函数关系式.
的函数关系式.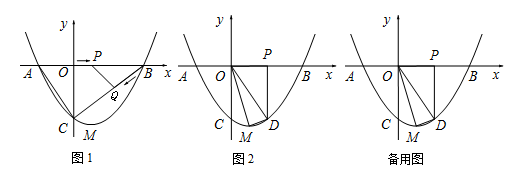
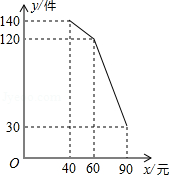
某商场销售一种商品的进价为每件30元,销售过程中发现月销售量 (件 与销售单价 (元 之间的关系如图所示.
(1)根据图象直接写出 与 之间的函数关系式.
(2)设这种商品月利润为 (元 ,求 与 之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
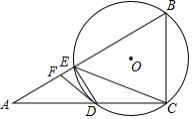
如图,在 中, , 是 上一点,过 , , 三点的 交 于点 ,连接 , ,点 是线段 上的一点,连接 ,其中 .
(1)求证: 是 的切线.
(2)若 是 的中点, , ,求 的长.
如图为某海域示意图,其中灯塔 的正东方向有一岛屿 .一艘快艇以每小时 的速度向正东方向航行,到达 处时测得灯塔 在东北方向上,继续航行 ,到达 处时测得灯塔 在北偏东 方向上,同时测得岛屿 恰好在 处的东北方向上,此时快艇与岛屿 的距离是多少?(结果精确到 .参考数据: , ,

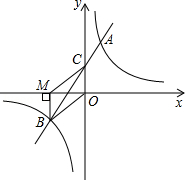
如图,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于 , 两点,点 在第一象限,纵坐标为4,点 在第三象限, 轴,垂足为点 , .
(1)求反比例函数和一次函数的解析式.
(2)连接 , ,求四边形 的面积.
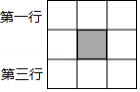
妈妈给小红和弟弟买了一本刘慈欣的小说《流浪地球》,姐弟俩都想先睹为快.于是小红对弟弟说:我们利用下面中心涂黑的九宫格图案(如图所示)玩一个游戏,规则如下:我从第一行,你从第三行,同时各自任意选取一个方格,涂黑,如果得到的新图案是轴对称图形,我就先读,否则你先读.小红设计的游戏对弟弟是否公平?请用画树状图或列表的方法说明理由.(第一行的小方格从左至右分别用 , , 表示,第三行的小方格从左至右分别用 , , 表示)