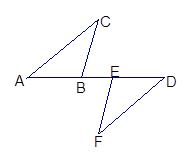
（·辽宁朝阳）问题：如图（1），在Rt△ACB中，∠ACB=90°，AC=CB，∠DCE=45°，试探究AD、DE、EB满足的等量关系．
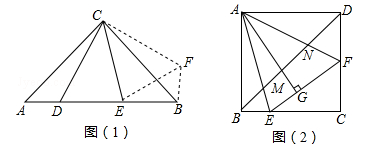
[探究发现]
小聪同学利用图形变换，将△CAD绕点C逆时针旋转90°得到△CBH，连接EH，由已知条件易得∠EBH=90°，∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°．根据“边角边”，可证△CEH≌ ，得EH=ED．
在Rt△HBE中，由 定理，可得BH2+EB2=EH2，由BH=AD，可得AD、DE、EB之间的等量关系是 ．
[实践运用]
（1）如图（2），在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等，求∠EAF的度数；
（2）在（1）条件下，连接BD，分别交AE、AF于点M、N，若BE=2，DF=3，BM=2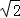
，运用小聪同学探究的结论，求正方形的边长及MN的长．
如图，△ABC与△ADE都是等边三角形（三条边都相等，三个内角都相等的三角形），连结BD、CE交点记为点F．
（1）BD与CE相等吗？请说明理由．
（2）你能求出BD与CE的夹角∠BFC的度数吗？
（3）若将已知条件改为：四边形ABCD与四边形AEFG都是正方形，连结BE、DG交点记为点M（如图）．请直接写出线段BE和DG之间的关系？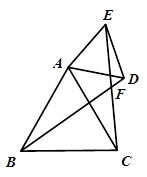
某公园门票是每人15元，若超过10人，可购买团体票，票价如下：
| 购买人数（人） |
10-50 |
51-100 |
100以上 |
| 每人门票价（元） |
13 |
11 |
9 |
有甲、乙两个旅游团，若分别购买门票，两团总计应付1314元；若合在一起购买门票，总计应付1008元，问这两个旅游团各有多少人？
一个不透明的口袋里装有红、白、黄三种颜色的乒乓球（除颜色外其余都相同），其中有白球2个，黄球1个．
（1）若口袋中有3个红球，求从任意摸出一个球是白球的概率，并用列表或画树状图的方法说明；
（2）若从袋中任意摸出一球，摸到白球的概率为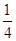
，求口袋中红球的个数．
在所给的网格图(每小格边长均为1的正方形)中，完成下列各题：
（1）将△ABC向右平移4个单位得到△A1B1C1；
（2）以直线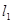
为对称轴作△ABC的轴对称图形△
；
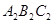（3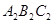）△可以看作是由△A1B1C1先向左平移4个单位，再以直线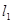为对称轴作轴对
称变换得到的。除此以外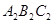，△还可以看作是由△A1B1C1经怎样变换得到的？请选择一种方法，写出图形变换的步骤。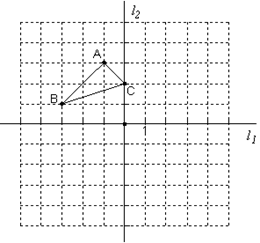
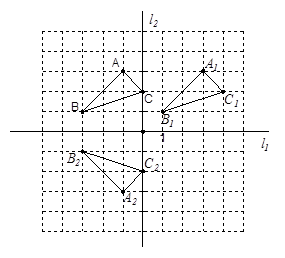
如图，在△ABC和△DEF中，∠A=∠D，AC=DF，AE=BD，请说明∠C=∠F的理由。