(·黑龙江大庆)如图,△ABC中,∠ACB=90°,D.E分别是BC、BA的中点,联结DE,F在DE延长线上,且AF=AE.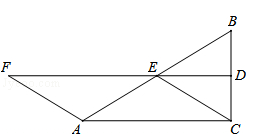
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
如果a,b互为相反数,c,d互为倒数,x的绝对值是1,求代数式 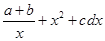 的值.
的值.
解比例或列比例并求x的值:(每题4分,共8分)
(1)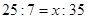
(2)比例式中,两个外项是x和36,两个内项是24和18.
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE,EF,FD之间的数量关系为.
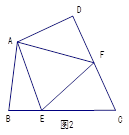
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=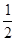 ∠BAD,线段BE,EF,FD之间存在什么数量关系,为什么?
∠BAD,线段BE,EF,FD之间存在什么数量关系,为什么?
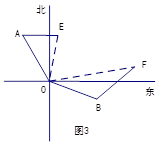
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达点E处,点B沿北偏东50°的方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.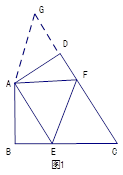
在正方形ABCD中,AB=4.
(1)正方形ABCD的周长为;
(2)如图1,点E 、F分别在BC和AD上,点P 是线段EF上的动点,过点P作
EF的垂线L,若直线L与正方形CD、AB两边的交点分别为G、H.
①求证:EF=GH;
②已知,BE=2,AF=1,若线段PE的长度为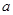 ,求
,求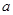 的最小值;
的最小值;
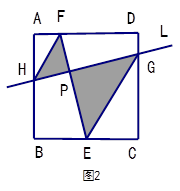
③如图2,在②的条件下,已知AH=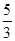 ,PE="2PF," 求图中阴影部分的面积.
,PE="2PF," 求图中阴影部分的面积.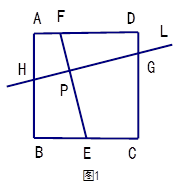
为了解市民的学习爱好,有关部门统计了最近6个月到图书馆的读者的职业
分布情况,并做了下列两个不完整的统计图.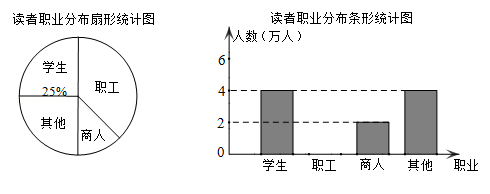
(1)本次共调查了多少人?
(2)将条形统计图补充完整;
(3)求“其它”所在扇形的圆心角的度数.