如图①,半径为R,圆心角为n°的扇形面积是 ,由弧长l=
,由弧长l= ,得
,得 =
= •
• •R=
•R= lR.通过观察,我们发现S扇形=
lR.通过观察,我们发现S扇形= lR类似于S三角形=
lR类似于S三角形= ×底×高.
×底×高.
类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分交作扇环)的面积公式及其应用.
(1)设扇环的面积为S扇环, 的长为
的长为 ,
, 的长为
的长为 ,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=
,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形= ×(上底+下底)×高,用含
×(上底+下底)×高,用含 ,
, ,h的代数式表示S扇环,并证明;
,h的代数式表示S扇环,并证明;
(2)用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?
如图, 为⊙O的直径,弦
为⊙O的直径,弦 于点
于点 ,过
,过 点作
点作 ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 。
。
(1)求证: 为⊙O的切线;
为⊙O的切线;
(2)如果 ,求⊙O的直径。
,求⊙O的直径。
把一副扑克牌中的3张黑桃牌(它们的正面牌面数字分别是3、4、5、)洗匀后正面朝下放在桌面上。
(1)如果从中抽取一张牌,那么牌面数字是4的概率是多少?
(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面数字。当2张牌面数字相同时,小王赢;当2张牌面数字不相同时,小李赢。现请你利用数状图或列表法分析游戏规则对双方是否公平?并说明理由。
某科技馆坐落在山坡M处,从山脚A处到科技馆的路线如图所示,已知A处在水平面上,斜坡AB的坡角为30°,AB=40m,斜坡BM的坡角为18°,BM=60m,那么科技馆M处的海拔高度是多少m?(精确到0.1m)(参考数据:sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
环境空气质量问题已成为人们日常生活所关心的重要问题,2012年2月,国务院发布的新修订的《环境空气质量标准》中增加了PM2.5的监测指标.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.环境检测中心今年在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5的监测.某日机抽取25个城市监测点的研究性数据,并绘制成统计表和扇形统计图如下: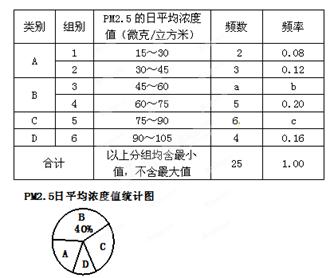
根据图表中提供的信息解答下列问题:
(1)统计表中的a=,b=,c=;
(2)在扇形统计图中,A类所对应的圆心角是度;
(3)我国PM2.5安全值的标准采用世界卫生组织(WHO)设定的最宽限值:日平均浓度小于75微克/立方米.请估计当日环保检测中心在监测的100个城市中,PM2.5日平均浓度值符合安全值的城市约有多少个?
如图,已知 的三个顶点的坐标分别为A(-2,3)、B(6,0)、C(-1,0).
的三个顶点的坐标分别为A(-2,3)、B(6,0)、C(-1,0).
(1)经过怎样的平移,可使 的顶点A与坐标原点O重合,并直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
的顶点A与坐标原点O重合,并直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
(2)将 绕坐标原点O逆时针旋转90°,得到△A′B′C′,画出△A′B′C′.
绕坐标原点O逆时针旋转90°,得到△A′B′C′,画出△A′B′C′.