（·辽宁辽阳）菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．
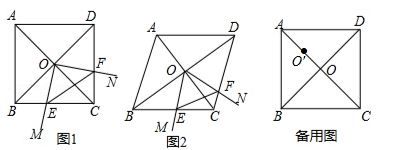
（1）如图1，当∠ABC=90°时，△OEF的形状是 ；
（2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；
（3）在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且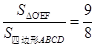
时，直接写出线段CE的长．
已知三角形第一边长为2
＋
，第二边比第一边长－，第三边比第二边短，求这个三角形的周长.
先化简，后求值：
，其中：
，
解一元一次方程：
计算：
请同学们认真阅读下面材料，然后解答问题。
解方程（x2－1）2－5（x－1）＋4＝0
解：设y＝x2－1
则原方程化为：y2－5y＋4＝0① ∴y1＝1 y2＝4
当y＝1时，有x2－1＝1，即x2＝2 ∴x＝±
当y＝4时，有x2－1＝4，即x2＝5∴x＝±
∴原方程的解为：x1＝－ x2＝ x3＝－ x4＝
解答问题：
⑴填空：在由原方程得到①的过程中，利用________________法达到了降次的目的，体现了________________的数学思想。
⑵解方程
－3（
－3）＝0