如图①，一次函数
的图象与二次函数
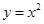的图象相交于A，B两点，点A，B的横坐标分别为m，n（m＜0，n＞0）．
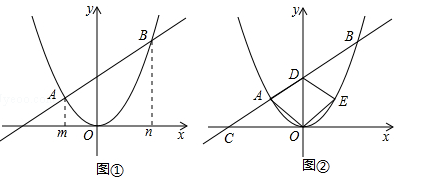
（1）当m=﹣1，n=4时，k= ，b= ；
当m=﹣2，n=3时，k= ，b= ；
（2）根据（1）中的结果，用含m，n的代数式分别表示k与b，并证明你的结论；
（3）利用（2）中的结论，解答下列问题：如图②，直线AB与x轴，y轴分别交于点C，D，点A关于y轴的对称点为点E，连接AO，OE，ED．
①当m=﹣3，n＞3时，求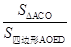
的值（用含n的代数式表示）；
②当四边形AOED为菱形时，m与n满足的关系式为 ；
当四边形AOED为正方形时，m= ，n= ．
如图，已知反比例函数
和一次函数y=2x-1，其中一次函数的图象经过（a，b），（a+1，b+k）两点。
（1）求反比例函数的解析式；
（2）如图，已知点A在第一象限，且同时在上述两个函数的图象上， 求点A的坐标；
（3）利用（2）的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标都求出来；若不存在，请说明理由。
一个不透明的口袋中有三个小球，上面分别标有数字1，2，3，每个小球，除数字外其他都相同．甲先从袋中随机取出1个小球，记下数字后放回；乙再从袋中随机取出1个小球记下数字．用画树状图或列表的方法，
（1）求取出的两个小球上的数字之和为3的概率；
（2）求取出的两个小球上的数字之和大于4的概率．
已知关于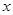
的一元二次方程
（
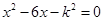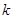为常数）．求证：方程有两个不相等的实数根．
解下列方程：
（1）2（x+2 ）2 －8 = 0
（2）（x+3）2 + 3（x+3）－4 = 0
A、B两站间的路程为448千米，一列慢车从A站出发，每小时行驶60千米；一列快车从B站出发，每小时行驶80千米，问：
（1）两车同时开出，相向而行，出发后多少小时相遇？
（2）两车相向而行，慢车先开出28分钟，快车开出后多少小时两车相遇？