如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM、射线AE于点F、D．
（1）直接写出∠NDE的度数；
（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由；
（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD=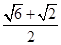 
，其他条件不变，求线段AM的长．
解方程：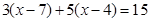
；
计算：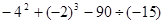
计算：8－23÷(－4)×(－7＋5)
A、B两地相距40千米，上午6时张强步行从A地出发于下午5时到达B地；上午10时王丽骑自行车从A地出发于下午3时到达B地，问王丽是在什么时间追上张强的？
某商场销售一种夹克和T恤，夹克每件定价100元，T恤每件定价50元，商场在开展促销活动期间，向顾客提供两种优惠方案.
方案一：买一件夹克送一件T恤
方案二：夹克和T恤均按定价的80%付款
现有顾客要到该商场购买夹克30件，T恤x件，（x＞30）
（1）若用方案一购买夹克需付款 元，T恤需付款（用含x的式子表示） 元，
若用方案二购买夹克需付款 元，T恤需付款（用含x的式子表示） 元；
（2）按方案一购买夹克和T恤共需付款 元，
按方案二购买夹克和T恤共需付款 元，
通过计算说明，购买多少件时，两种方案付款一样多？
（3）当x＝40时，你能给出一种更省钱的方案吗？写出你的方案.