如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且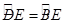 。
。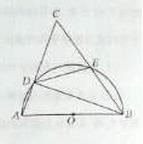
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求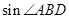 的值。
的值。
计算:(1)
(2)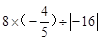
(3)
(4)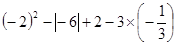
(5)
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
已知,如图,四边形 中,
中, ,
, ,
,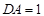 ,且
,且 ,
,
试求:(1) 的度数;(2)四边形
的度数;(2)四边形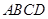 的面积(结果保留根号);
的面积(结果保留根号);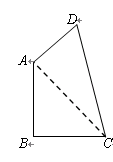
已知:2m+2的平方根是±4,3m+n+1的平方根是±5,求m+2n的值
如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.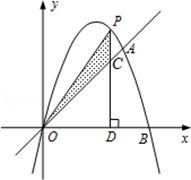
(1)求出二次函数的解析式;
(2)当点P在直线OA的上方时,用含m的代数式表示线段PC的长,并求线段PC的最大值;
(3)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,如果存在,请直接写出所有P的坐标;如果不存在,请说明理由.