某质点做直线运动,其位移x与时间t的关系图像如图所示。则
| A.在12s时刻质点开始做反向的直线运动 |
| B.在0~20s内质点的速度不断增加 |
| C.在0~20s内质点的平均速度大小为0.8m/s |
| D.在0~20s内质点的瞬时速度等于它在这段时间内平均速度的时刻只有一处 |
放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间t的关系如图所示.取重力加速度g=10m/s2.由此两图线可以求得物块的质量m和物块与地面之间的动摩檫因数μ分别为()
A. |
B. |
C. |
D. |
下列说法叙述正确的是()
| A.牛顿发现了万有引力定律 | B.库仑通过实验测出了元电荷的带电量 |
| C.伽利略发现了行星运动的规律 | D.奥斯特发现了电磁感应定律 |
如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度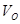 沿水平射中木块,并最终留在木块中与木块一起以速度v运动.已知当子弹相对木块静止时,木块前进距离L,子弹进入木块的深度为s.若木块对子弹的阻力f视为恒定,则下列关系式中不正确的是()
沿水平射中木块,并最终留在木块中与木块一起以速度v运动.已知当子弹相对木块静止时,木块前进距离L,子弹进入木块的深度为s.若木块对子弹的阻力f视为恒定,则下列关系式中不正确的是()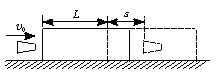
A.fL=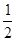 Mv2 Mv2 |
B.f(L+s)=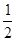 mv02- mv02-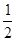 mv mv |
C.fs=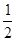 mv02- mv02-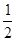 (M+m)v2 (M+m)v2 |
D.fs=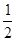 mv2 mv2 |
如图所示,当用力F将B向右拉动时,有关力做功的说法正确的是()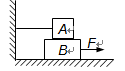
| A.F做正功,A、B受到的摩擦力均不做功 |
| B.绳拉力、A受到的摩擦力均不做功 |
| C.F做正功,A、B受到的摩擦力均做负功 |
| D.F做正功,B受到的摩擦力做负功 |
关于匀速圆周运动的线速度,下列说法中正确的是
| A.大小和方向都保持不变 |
| B.大小不变,方向时刻改变 |
| C.大小时刻改变,方向不变 |
| D.大小和方向都时刻改变 |