（广安）如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：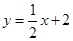
经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线
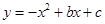顶点E在直线l上．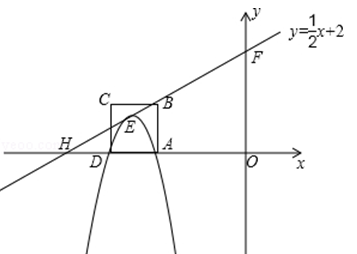
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当抛物线顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．
如图，道路边有一棵树，身高1.8米的某人站在水平地面的D点处，从C点测得树的顶端A点的仰角为60°，树的底部B点的俯角为30°，求树的高度AB．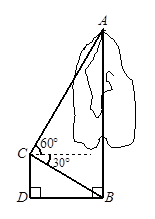
在三个不透明的袋子中分别装有一些除颜色外完全相同的球．甲袋中装有1个红球和2个白球，乙袋中装有1个黄球和1个白球，丙袋中装有1个红球和1个白球．从每个袋子中随机摸出一个球，用树形图法求“摸出三个白球”的概率．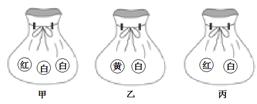
如图，在平面直角坐标系中，A（-1，1），B（-2，-1）．（1）以原点O为位似中心，把线段AB放大到原来的2倍，请在图中画出放大后的线段CD；（2）在（1）的条件下，写出点A的对应点C的坐标为，点B的对应点D的坐标为．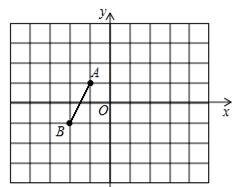
在二次函数
中，函数y与自变量x的部分对应值如下表：
| x |
… |
－1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
8 |
3 |
0 |
－1 |
0 |
… |
（1）求这个二次函数的表达式；
（2）当x的取值范围满足什么条件时，
？
如图，⊙O的半径为3，点P是弦AB延长线上的一点，连接OP，若OP=4，∠P=30°，求弦AB的长.