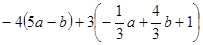(广安)如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数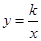 (
(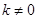 )的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.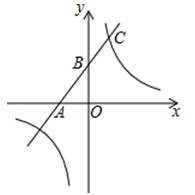
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
| 排数 |
1 |
2 |
3 |
4 |
| 座位数 |
50 |
53 |
56 |
59 |
按这种方式排下去,
(1)第5、6排各有多少个座位?
(2)第n排有多少个座位?
(3)根据(2)的代数式,判断第25排有多少个座位?
小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:厘米):
+4,-3, +10,-8, -5, +12,-10
问:(1)小虫是否回到原点O ?
(2)小虫离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则小虫共可得到多少粒芝麻?
先化简再求值: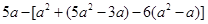 ,其中
,其中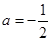
已知b、c互为相反数,m、n互为倒数,x的绝对值为2.求代数式 的值.
的值.
化简:(1) (2)
(2)