（攀枝花）“热爱劳动，勤俭节约”是中华民族的光荣传统，某小学校为了解本校3至6年级的3000名学生帮助父母做家务的情况，以便做好引导和教育工作，随机抽取了200名学生进行调查，按年级人数和做家务程度，分别绘制了条形统计图（图1）和扇形统计图（图2）．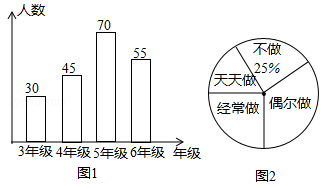
（1）四个年级被调查人数的中位数是多少？
（2）如果把“天天做”、“经常做”、“偶尔做”都统计成帮助父母做家务，那么该校3至6年级学生帮助父母做家务的人数大约是多少？
（3）在这次调查中，六年级共有甲、乙、丙、丁四人“天天帮助父母做家务”，现准备从四人中随机抽取两人进行座谈，请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率．
AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
（1）若∠AOD=52°，求∠DEB的度数；
（2）若OC=3，OA=5，求AB的长．
列方程解应用题：
如图，有一块矩形纸板，长为20
，宽为14，在它的四角各切去一个同样的正方形，然后将四周突出部分沿虚线折起；就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为160
，那么纸板各角应切去边长为多大的正方形?
如图，Rt△ABC中，∠C=90°，∠A=30°，AB=2．
（1）用尺规作图，作出△ABC绕点A逆时针旋转60°后得到的AB1Cl（不写画法，保留图画痕迹）；
结论：__________为所求．
（2）在（1）的条件下，连接B1C，求B1C的长．
下图是4×4的正方形网格，请在其中选取一个白色的单位正方形并涂黑，使图中黑色部分是一个中心对称图形．
如图，AB为⊙O的弦，AB=8，OC⊥AB于点D，交⊙O于点C，且CD=1，求⊙O的半径。