(凉山州)阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF= (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点
请你运用所学知识,结合上述材料,解答下列问题.
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD= ,OC=5,求MN的长.
,OC=5,求MN的长.
如图,直线MN与直线PQ垂直相交于点O,点A在直线PQ上运动,点B在直线MN上运动.
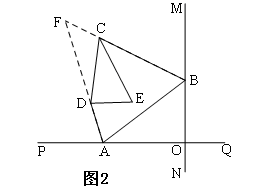
(1) 如图1,已知AE、BE分别是∠BAO和∠ABO的角平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,请说明理由,并求出∠AEB的大小.
(2) 如图2,已知AB不平行CD, AD、BC分别是∠BAP和∠ABM的角平分线,AD、BC的延长线交于点F.∠ADC的角平分线DE和∠BCD的角平分线CE相交于点E.
① 点A、B在运动的过程中,∠F的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,请说明理由.
② 点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,请说明理由.
“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2) 预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
如图,D是△ABC的BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=63°.求∠DAC的度数.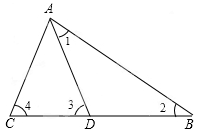
甲、乙两个车间工人人数不相等,若甲车间调10人到乙车间,则两车间人数相等;若乙车间调10人到甲车间,则甲车间的人数就是乙车间人数的2倍,求原来甲、乙两车间各有多少名工人?
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表: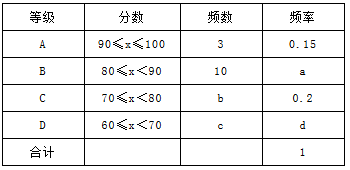
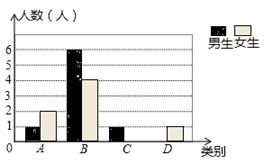
请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.