（成都）（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线
（
）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：
与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；
（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为
，求a的值；
（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．
如图，直线AB、CD相交于O，∠BOC＝800，OE是∠BOC的角平分线，OF是OE的反向延长线．
（1）求∠2、∠3的度数；
（2）试说明：OF平分∠AOD
有这样一道题目：“当a＝0.35，b＝－0.28时，求多项式
7a－3(2ab－ab－a)＋(6ab－3ab)－(10a－3)的值”．小敏指出，题中给出的条件a＝0.35，b＝－0.28是多余的，她的说法有道理吗？为什么？
数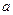
，
，
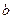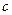在数轴上的位置如图所示且
；
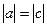（1）若
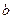，求的值；
（2）用“>”从大到小把a，b，-b，c连接起来；
已知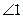
、线段AB及射线OM，按下列要求画图：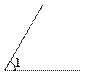
（1）在射线OM上取一点C，使OC＝AB；
（2）画
；
（3）在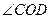
的边OD上取一点E，使OE＝2AB；
（4）测量点E与点C之间的距离为 cm（精确到1cm）.
（每小题5分,共10分）
计算：
（1）
；
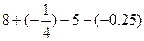（2）
.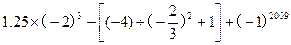