(·台州市 第24题 14分)定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBM均是等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究 ,
, 和
和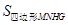 的数量关系,并说明理由
的数量关系,并说明理由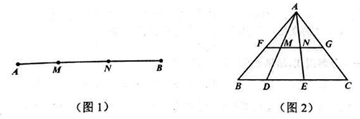

(本题10分)我校八年级举行英语风采演讲比赛,派两位老师去超市购买笔记本作为奖品.据了解,该超市的甲、乙两种笔记本的价格分别是10元和6元,他们准备购买这两种笔记本共30本.
(1)若这两位老师计划用220元购买奖品,则能买这两种笔记本各多少本?
(2) 若他们根据演讲比赛的设奖情况,决定所购买的甲种笔记本的数量不多于乙种笔记本数量的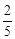 ,但又多于乙种笔记本数量的
,但又多于乙种笔记本数量的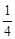 ,若设他们买甲种笔记本x本,买这两种笔记本共花费y元.
,若设他们买甲种笔记本x本,买这两种笔记本共花费y元.
①求出y(元)关于x(本)的函数关系式;
②问购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
如图,已知 的中垂线
的中垂线 交
交 于点
于点 ,交
,交 于点
于点 ,有下面3个结论:
,有下面3个结论:
① 是等腰三角形;
是等腰三角形;
② ∽
∽ ;
;
③点D是线段AC的黄金分割点.
请你从以上结论中只选一个加以证明
(友情提醒:证明①得8分,证明②得10分,证明③得12分).
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数 的图象的两个交点.
的图象的两个交点.
(1) 求此反比例函数的解析式及n的值;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
小美有红色、白色、蓝色上衣各一件,黄色、黑色长裤各一条.
(1)请用画树状图或列表的方法分析小美上衣和长裤有多少种不同的搭配情况;
(2)其中小美穿蓝色上衣的概率是多少?
如图,∠ABC=∠CDB=90°,AC=a,BC=b.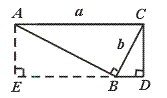
(1)当BD与a、b之间满足怎样的关系时,△ABC∽△CDB?
(2)过A作BD的垂线,与DB的延长线交于点E,若△ABC∽△CDB.求证四边形AEDC为矩形(自己完成图形).