（·湖北黄冈，15题，分）解不等式组：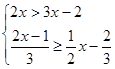
．
某校同学参加语文知识竞赛，将学生的成绩，进行整理后分成5组，绘制成频数分布直方图如下，图中从左到右各小组的频率分别是0．0625，0．25，0．375，0．1875，0．125且已知最右边小组的频数为6，结合直方图提供的信息，解答下列问题：
（1）该校参加语文知识竞赛学生共有多少人？
（2）成绩落在哪组数据范围内的人数最多？是多少？
（3）求成绩在80分以下的学生人数．
节日某品牌服装打折，小明去购买了一套衣服共花了400元，已知上衣打八折，裤子打七折，上衣与裤子总价格为540元，求上衣与裤子原价各是多少元．
解方程：
（1）
（x-3）=（x+4）-
（2）
-
=1
尺规作图（要求保留作图痕迹）：已知：线段a，b．求作：线段c，使得c=2b-a．
先化简，后求值：2（x2-6y）-（4x2+3y-1），其中x=
，y=-
．