如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=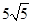
，且
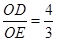，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：
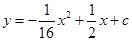经过点E，且与AB边相交于点F．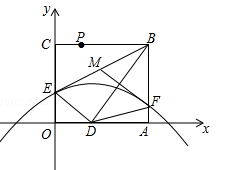
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．
已知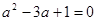
，求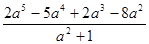
已知多项式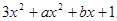
能被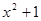
整除且商式是
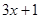，求
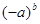的值。
观察下列等式：
第1 个等式：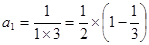
；
第2个等式：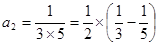
；
第3个等式：
；
第4个等式：
；
……
请解答下列问题：
（1）按以上规律列出第5个等式：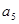
=_______=_________；
（2）用含有n的代数式表示第n个等式：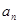
=_________=__________（n为正整数）；
（3）求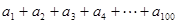
．
某地上网有两种收费方式，用户可以任选其中一种：
方式一，记时制：2.5元/小时；
方式二，包月制：60元/月．此外，每一种上网方式都加收通信费1元/小时．
（1）某用户上网20小时，选用哪种上网方式比较合算？说明你的理由；
（2）某用户有140元钱用于上网（一个月），选用哪种方式比较合算？说明你的理由；
（3）请你为用户设计一个方案，使用户能合理地选择上网方式．
某车间有技工85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配一套，问加工甲、乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套？