如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据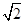 ≈1.4,
≈1.4,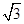 ≈1.7)
≈1.7)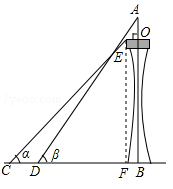
公司2018年使用自主研发生产的“ ”系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲、乙两类芯片产量的和还多400万块.这些“ ”芯片解决了该公司2018年生产的全部手机所需芯片的 .
(1)求2018年甲类芯片的产量;
(2) 公司计划2020年生产的手机全部使用自主研发的“ ”系列芯片.从2019年起逐年扩大“ ”芯片的产量,2019年、2020年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数 ,乙类芯片的产量平均每年增长的百分数比 小1,丙类芯片的产量每年按相同的数量递增 年到2020年,丙类芯片三年的总产量达到1.44亿块.这样,2020年的 公司的手机产量比2018年全年的手机产量多 ,求丙类芯片2020年的产量及 的值.
如图,点 是线段 上一点, ,以点 为圆心, 的长为半径作 ,过点 作 的垂线交 于 , 两点,点 在线段 的延长线上,连接 交 于点 ,以 , 为边作 .
(1)求证: 是 的切线;
(2)若 ,求四边形 与 重叠部分的面积;
(3)若 , ,连接 ,求 和 的长.

某校在参加了宜昌市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度“阅读素养、数学素养、科学素养、人文素养”,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).小明、小颖和小雯在协助老师进行统计后,有这样一段对话:
小明:“选科学素养和人文素养的同学分别为16人,12人.”
小颖:“选数学素养的同学比选阅读素养的同学少4人.”
小雯:“选科学素养的同学占样本总数的 .”
(1)这次抽样调查了多少名学生?
(2)样本总数中,选“阅读素养”、“数学素养”的学生各多少人?
(3)如图是调查结果整理后绘制成的扇形图.请直接在横线上补全相关百分比;
(4)该校八年级有学生400人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?

《人民日报》点赞湖北宜昌“智慧停车平台”.作为“全国智慧城市”试点,我市通过“互联网”、“大数据”等新科技,打造“智慧停车平台”,着力化解城市“停车难”问题.市内某智慧公共停车场的收费标准是:停车不超过30分钟,不收费;超过30分钟,不超过60分钟,计1小时,收费3元;超过1小时后,超过1小时的部分按每小时2元收费(不足1小时,按1小时计).
(1)填空:若市民张先生某次在该停车场停车2小时10分钟,应交停车费 元.若李先生也在该停车场停车,支付停车费11元,则停车场按 小时(填整数)计时收费.
(2)当 取整数且 时,求该停车场停车费 (单位:元)关于停车计时 (单位:小时)的函数解析式.
如图,在 中, 是 边上的一点, , 平分 ,交 边于点 ,连接 .
(1)求证: ;
(2)若 , ,求 的度数.
