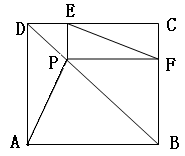
如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)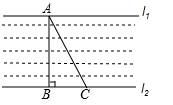
已知关于 的一元二次方程x2+2x+2k-4=0
的一元二次方程x2+2x+2k-4=0 有两个不相等的实数根。
有两个不相等的实数根。
(1)求 的取值范围;
的取值范围;
(2)若k为正整数,且该方程的根都是整数,求 的值。
的值。
(1)解不等式组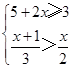 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
(2)某园林队计划由6名工人对180平方米的区域进行绿化,由于施工时增加了2名工人,结果比计划提前3小时完成任务。若每人每小时绿化面积相同,求每人每小时的绿化面积。
(1)计算: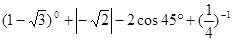 ;
;
(2)先化简,再求值: ,其中x是方程
,其中x是方程 的根.
的根.
阅读下列解题过程: ;
;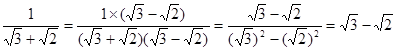 .
.
利用上面所提供的解法,化简 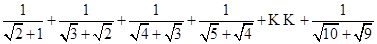
(2)观察上面的解题过程,请直接写出: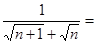 。(n为正整数)
。(n为正整数)
已知:如图,正方形ABCD中,P是对角线BD上的一个动点,PE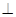 CD于E, PF
CD于E, PF BC于F,连接EF,求证:AP=EF.
BC于F,连接EF,求证:AP=EF.