在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF-优题课

在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．
（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；
（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：；
（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．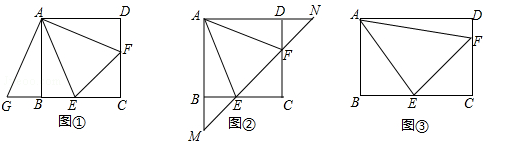

科目数学题型解答题难度中等

如图，点 $A$ 、 $B$ 在数轴上，它们对应的数分别为 $- 2$ ， $\frac{x}{x + 1}$ ，且点 $A$ 、 $B$ 到原点的距离相等．求 $x$ 的值．

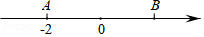
计算： ${(\frac{1}{2})}^{- 1} - {(2019 - π)}^{0} + 2 \sin 30 °$ ．

如图，直线 $y = - x + 4$ 与 $x$ 轴， $y$ 轴分别交于 $A$ ， $B$ 两点，过 $A$ ， $B$ 两点的抛物线 $y = a x^{2} + bx + c$ 与 $x$ 轴交于点 $C (- 1, 0)$ ．

（1）求抛物线的解析式；

（2）连接 $BC$ ，若点 $E$ 是线段 $AC$ 上的一个动点（不与 $A$ ， $C$ 重合），过点 $E$ 作 $EF / / BC$ ，交 $AB$ 于点 $F$ ，当 $ΔBEF$ 的面积是 $\frac{5}{2}$ 时，求点 $E$ 的坐标；

（3）在（2）的结论下，将 $ΔBEF$ 绕点 $F$ 旋转 $180 °$ 得△ $B' E' F$ ，试判断点 $E'$ 是否在抛物线上，并说明理由．

如图， $AB$ 是 $⊙ O$ 的直径，点 $P$ 是 $BA$ 延长线上一点，过点 $P$ 作 $⊙ O$ 的切线 $PC$ ，切点是 $C$ ，过点 $C$ 作弦 $CD ⊥ AB$ 于 $E$ ，连接 $CO$ ， $CB$ ．

（1）求证： $PD$ 是 $⊙ O$ 的切线；

（2）若 $AB = 10$ ， $\tan B = \frac{1}{2}$ ，求 $PA$ 的长；

（3）试探究线段 $AB$ ， $OE$ ， $OP$ 之间的数量关系，并说明理由．

如图，在平面直角坐标系中，直线 $AB$ 与 $y$ 轴交于点 $B (0, 7)$ ，与反比例函数 $y = \frac{- 8}{x}$ 在第二象限内的图象相交于点 $A (- 1, a)$ ．

（1）求直线 $AB$ 的解析式；

（2）将直线 $AB$ 向下平移9个单位后与反比例函数的图象交于点 $C$ 和点 $E$ ，与 $y$ 轴交于点 $D$ ，求 $ΔACD$ 的面积；

（3）设直线 $CD$ 的解析式为 $y = mx + n$ ，根据图象直接写出不等式 $mx + n ⩽ \frac{- 8}{x}$ 的解集．

试卷网试题网古诗词网作文网范文网