某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数
（张）与售票时间x（小时）的变化趋势如图1，每个无人售票窗口售出的车票数
（张）与售票时间x（小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．
（1）求图2中所确定抛物线的解析式；
（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？
如图，在直角梯形ABCD中，AB∥DC，AB⊥BC，∠A=60°，AB=2CD，E、F分别为AB、AD的中点，联结EF、EC、BF、CF．四边形AECD的形状是；
若CD=2，求CF的长．
小明从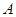
地出发向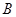
地行走，同时晓阳从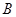地出发向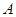地行走，如图所示，相交于点M的两条线段
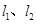分别表示小明、晓阳离A地的距离
（千米）与已用时间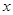
（分钟）之间的关系，小明与晓阳相遇时，晓阳出发的时间是；
求小明与晓阳的速度。
已知一次函数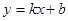
的图像经过点A(1，0)和B
（
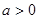），且点B在反比例函数
的图像上．求一次函数的解析式；
若点M是
轴上一点，且满足△ABM是直角三角形，请直接写出点M的坐标．
如图，∠ACB=∠CDE=90°，B是CE的中点，∠DCE=30°，AC=CD．求证：AB∥DE．
在一个三角形中，如果一个角是另一个角的2倍，我们称这种三角形为倍角三角形．如图28-1，倍角△ABC中，∠A=2∠B，∠A、∠B、∠C的对边分别记为a,b,c，倍角三角形的三边a,b,c有什么关系呢？让我们一起来探索．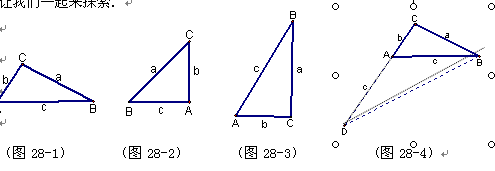
我们先从特殊的倍角三角形入手研究.请你结合图形填空：
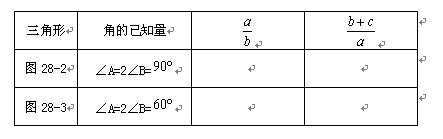
如图28-4，对于一般的倍角△ABC，若∠CAB=2∠CBA ，∠CAB、∠CBA、∠C的对边分别记为a、b、c，a、b、c三边有什么关系呢？请你作出猜测，并结合图28-4给出的辅助线提示加以证明．