(1)如图1是某个多面体的表面展开图.
①请你写出这个多面体的名称,并指出图中哪三个字母表示多面体的同一点;
②如果沿BC、GH将展开图剪成三块,恰好拼成一个矩形,那么△BMC应满足什么条件?(不必说理)
(2)如果将一个三棱柱的表面展开图剪成四块,恰好拼成一个三角形,如图2,那么该三棱柱的侧面积与表面积的比值是多少?为什么?(注:以上剪拼中所有接缝均忽略不计)
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
平行四边形两个顶点坐标分别为(-3,0),(1,0),第3个顶点在y轴上,且与x轴的距离为3个单位长度.求第4个顶点的坐标.
如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的路程S与该日下午时间t之间的关系,试根据图形回答:
(1)甲出发几小时,乙才开始出发?
(2)乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
(3)甲从下午2时到5时的速度是多少?
(4)乙行驶的速度是多少?
如图,已知在△ABC中,∠ACB=90°,点D、E、F分别是AC、AB、BC的中点,
试说明:CE=DF.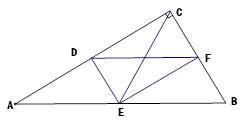
如图,在△ABC中,A(−2,3),B(−3,1),C(−1,2).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)将△ABC绕原点O旋转180°,画出旋转后的△A2B2C2;
(3)若P(m,n)为AB边上任一点,写出△A2B2C2中与P点对应的点坐标.