定义:长宽比为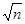
：1（n为正基数）的矩形称为株为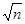矩形．下面，我们通过折叠的方式折出一个
矩形．如图①所示．
操作1：将正方形ABCD沿过点B的直线折叠，使折叠后的点C落在对角线BD上的点G处，折痕为BH
操作2：将AD沿过点G的直线折叠，使点A，点D分别落在边AB，CD上，折痕为EF
则四边形BCEF为矩形
证明：设正方形ABCD的边长为1，则BD=
=．
由折叠性质可知BG=BC=1，
，则四边形BCEF为矩形
阅读以上内容，回答下列问题：
在图
中，所有与CH相等的线段是 ，tan
的值是
已知四边形BCEF为矩形，模仿上述操作，得到四边形BCMN，如图
。
求证：四边形BCMN是
矩形
将图中的矩形BCMN沿用（2）中的操作3次后，得到一个“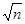矩形”，则n的值是
＋(－
)＋2
