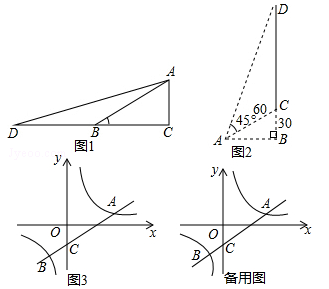
理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC= .tanD=tan15°=
.tanD=tan15°=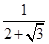 =
=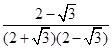 =
=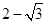 .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=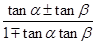 .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=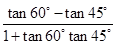 =
=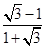 =
=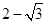 .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线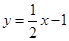 与双曲线
与双曲线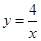 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
已知直线 分别与
分别与 轴、
轴、 轴交于点
轴交于点 、
、 ,抛物线
,抛物线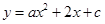 经过点
经过点 、
、 .
.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线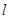 ,点
,点 关于直线
关于直线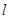 的对称点为
的对称点为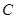 ,若点
,若点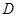 在
在 轴的正半轴上,且四边形
轴的正半轴上,且四边形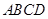 为梯形.
为梯形.
① 求点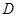 的坐标;
的坐标;
② 将此抛物线向右平移,平移后抛物线的顶点为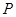 ,其对称轴与直线
,其对称轴与直线 交于点
交于点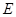 ,若tan
,若tan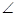
 =
=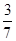 ,求四边形
,求四边形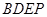 的面积.
的面积.
如图,在梯形 中,
中, ∥
∥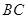 ,
,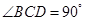 ,
,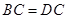 ,点
,点 在对角线
在对角线 上,作
上,作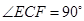 ,连接
,连接 ,且满足
,且满足 .
.
(1)求证: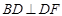 ;
;
(2)当 时,试判断四边形
时,试判断四边形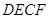 的形状,并说明理由.
的形状,并说明理由.
随着“微博潮”的流行,初中学生也开始忙着“织围脖”,某校在上微博的280名学生中随机抽取了部分学生调查他们平常每天上微博的时间,绘制了扇形统计图和频数分布直方图,请根据图中信息,回答下列问题: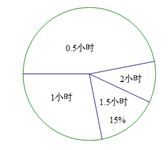
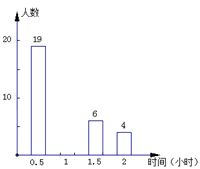
(1)本次共抽取了名学生,将频数分布直方图补充完整;
(2)被调查的学生中上微博的时间中位数落在这一小组内;
(3)样本中,平均每天上微博的时间为0.5小时这一组的频率是;
(4)请估计该校上微博的学生中,大约有名学生平均每天上微博的时间不少于1小时;
某公园有一圆弧形的拱桥,如图已知拱桥所在的圆的半径为10米,拱桥顶 到水面
到水面 距离
距离 米.
米.
(1)求水面宽度 的大小;
的大小;
(2)当水面上升到 时,从点
时,从点 测得桥顶
测得桥顶 的仰角为
的仰角为 ,若
,若 =3,求水面上升的高度.
=3,求水面上升的高度.
解方程组: .
.