如图，抛物线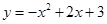
与x轴交于A，B两点，与y轴交于点C，点D为抛物线的顶点，请解决下列问题．
（1）填空：点C的坐标为（ ，），点D的坐标为（ ，）；
（2）设点P的坐标为（a，0），当
最大时，求a的值并在图中标出点P的位置；
（3）在（2）的条件下，将△BCP沿x轴的正方向平移得到△B′C′P′，设点C对应点C′的横坐标为t（其中0＜t＜6），在运动过程中△B′C′P′与△BCD重叠部分的面积为S，求S与t之间的关系式，并直接写出当t为何值时S最大，最大值为多少？
计算（每小题4分，共8分）
（1）
＋|1－
|－
－（π－1）0
（2）
-
已知点A（a，2014）与点B（2015，b）关于x轴对称，则a＋b的值为（）
如图，在四边形ABCD中，AB＝DC，延长线段CB到E，使BE＝AD，连接AE、AC，且AE＝AC．
求证：（1）△ABE≌△CDA；
（2）AD∥EC．
△ABC在平面直角坐标系xOy中的位置如图所示．
（1）作△ABC关于y轴成轴对称的△A1B1C1；
（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2；则此三角形的面积为 ．
（3）在x轴上求作一点P，使PA1+PC2的值最小，点P的坐标为 ．
（每小题3分，共6分）求下列各式中的x．
（1）
（2）
．