(钦州)某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元?
已知关于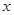 的方程
的方程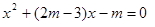 的两个不相等的实数根为
的两个不相等的实数根为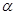 、
、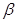 满足
满足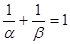 ,求
,求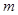 的值.
的值.
如图,数轴上点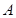 表示的数为
表示的数为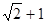 ,点
,点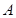 在数轴上向左平移
在数轴上向左平移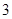 个单位到达点
个单位到达点 ,点
,点 表示的数为
表示的数为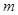 .
.
求
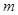 的值
的值化简:
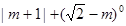
如图,直线 与
与 轴交于
轴交于 ,与
,与 轴交于
轴交于 ,以
,以 为边作矩形
为边作矩形 ,点
,点 在
在 轴上,双曲线
轴上,双曲线 经过点
经过点 与直线
与直线 交于
交于 ,
, 轴于
轴于 ,则
,则 .
.
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。①当点
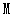 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点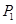 、
、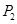 ,则
,则 (,)、
(,)、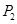 (,);②当∠OMN=60°时,对应的点P是点
(,);②当∠OMN=60°时,对应的点P是点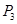 ,求
,求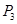 的坐标;
的坐标;若抛物线
 ,是经过(1)中的点
,是经过(1)中的点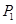 、
、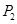 、
、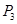 ,试求a、b、c的值;
,试求a、b、c的值;在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用
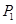 、
、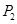 、
、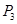 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
观察发现
如题27(a)图,若点A,B在直线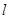 同侧,在直线
同侧,在直线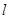 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线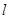 的对称点
的对称点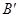 ,连接
,连接 ,与直线
,与直线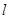 的交点就是所求的点P
的交点就是所求的点P
再如题27(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这
点就是所求的点P,故BP+PE的最小值为.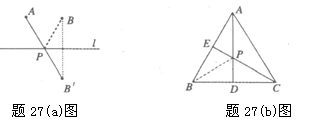
实践运用
如题27(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.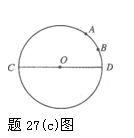
拓展延伸
如题27(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.