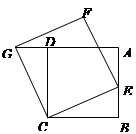（桂林）如图，已知抛物线
与坐标轴分别交于点A（0，8）、B（8，0）和点E，动点C从原点O开始沿OA方向以每秒1个单位长度移动，动点D从点B开始沿BO方向以每秒1个单位长度移动，动点C、D同时出发，当动点D到达原点O时，点C、D停止运动．
（1）直接写出抛物线的解析式： ；
（2）求△CED的面积S与D点运动时间t的函数解析式；当t为何值时，△CED的面积最大？最大面积是多少？
（3）当△CED的面积最大时，在抛物线上是否存在点P（点E除外），使△PCD的面积等于△CED的最大面积？若存在，求出P点的坐标；若不存在，请说明理由．
将分别标有数字1，2，3 的三张卡片洗匀后，背面朝上放在桌面上.
（1）随机抽取一张，求抽到奇数的概率；
（2）随机抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，能组成哪些两位数？恰好是32的概率是多少.
如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：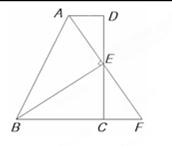
（1）FC=AD；
（2）AB=BC+AD.
如图，△ABC中，BD、CE是△ABC的两条高，点F、M分别是DE、BC的中点. 求证：FM⊥DE.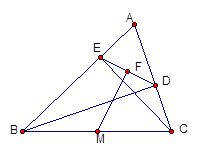
某池塘里养了鱼苗1万条，根据这几年的经验，鱼苗成活率为95%，一段时间后准备打捞出售，第一网捞出40条，称得平均每条鱼重2.5千克，第二网捞出25条，称得平均每条鱼重2.2千克，第三网捞出35条，称得平均每条鱼重2.8千克，试估计这池塘中鱼的质量.
如图，已知正方形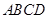
中，点
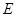是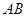
上的一点，连结
，以为一边，在的上方作正方形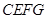
，连结
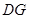．求证：
.