（钦州）如图，在平面直角坐标系中，以点B（0，8）为端点的射线BG∥x轴，点A是射线BG上的一个动点（点A与点B不重合）．在射线AG上取AD=OB，作线段AD的垂直平分线，垂足为E，且与x轴交于点F，过点A作AC⊥OA，交射线EF于点C．连接OC、CD，设点A的横坐标为t．
（1）用含t的式子表示点E的坐标为_______；
（2）当t为何值时，∠OCD=180°？
（3）当点C与点F不重合时，设△OCF的面积为S，求S与t之间的函数解析式．
先化简
÷
•
(1+
)，若结果等于
，求出相应的
的值．
下面是我县某养鸡场2001～2006年的养鸡统计图：
（1）从图中你能得到什么信息.
（2）各年养鸡多少万只？
（3）所得（2）的数据都是准确数吗？
（4）这张图与条形统计图比较，有什么优点？
完成下列证明（每空1分，共7分）
在括号内填写理由.（1） 如图，已知∠B+∠BCD=180°，∠B=∠D. 求证：∠E=∠DFE.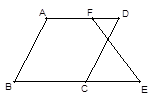 
证明：∵∠B+∠BCD=180°( ),
∴AB∥CD （）
∴∠B=∠DCE（）
又∵∠B=∠D（）,
∴∠DCE=∠D ()
∴AD∥BE（）
∴∠E=∠DFE（）
、如图，已知：∠1=120°，∠C=60°。说明AB∥CD理由。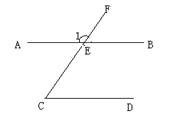
.已知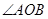
,利用尺规作
,使得=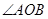
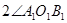（要求不写做法，但要保留做图痕迹）