(梧州)已知AB是⊙O的直径,CD是⊙O的弦,AB与CD交于E,CE=DE,过B作BF∥CD,交AC的延长线于点F,求证:BF是⊙O的切线.
作出下列图形的所有对称轴.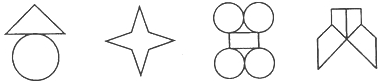
请你在纸上画一个等腰三角形ABC(如图),使得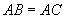 .
.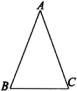
(1)请你判断一下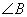 与
与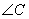 有什么大小关系呢?你的依据是什么?
有什么大小关系呢?你的依据是什么?
(2)请你再深入地思考一个问题:若只知道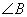 与
与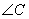 相等,请你判断一下这个三角形是什么形状的呢?并说明你的探索思路.
相等,请你判断一下这个三角形是什么形状的呢?并说明你的探索思路.
(3)由第(2)你会得到一个什么结论呢?请用一句话概括出来.
(4)现在给出两个三角形(如图),请你把图(1)分割成两个等腰三角形,把图(2)分割成三个等腰三角形.动动脑筋呀!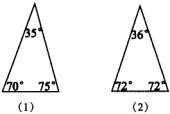
有一个三角形的支架如图所示,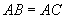 ,小明过点A和BC边的中点D又架了一个细木条,经测量
,小明过点A和BC边的中点D又架了一个细木条,经测量 ,你在不用任何测量工具的前提下,能得到
,你在不用任何测量工具的前提下,能得到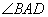 和
和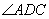 的度数吗?
的度数吗?
如图,已知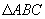 中,DE垂直平分AC,交C于点E,交BC于点D,
中,DE垂直平分AC,交C于点E,交BC于点D,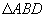 的周长是20厘米,AC长为8厘米,你能判断出
的周长是20厘米,AC长为8厘米,你能判断出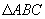 的周长吗?试试看.
的周长吗?试试看.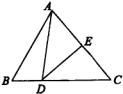
老师正叙述这样一道题:请同学们画出一个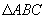 ,然后画出
,然后画出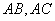 的中垂线,且交于点P.请同学们想一下点P到三角形三个顶点
的中垂线,且交于点P.请同学们想一下点P到三角形三个顶点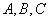 的距离如何?小明马上就说:“相等.”他是随便说的吗?你同意他的说法吗?请说明你的理由.
的距离如何?小明马上就说:“相等.”他是随便说的吗?你同意他的说法吗?请说明你的理由.