(来宾)在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)
为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1-5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:
(1)某镇今年1-5月新注册小型企业一共有 家.请将折线统计图补充完整;
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
已知关于x的方程mx2-(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都0是整数,求正整数m的值.
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,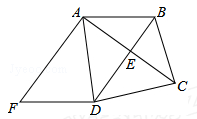
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.