(河池)如图1,抛物线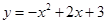 与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
解下列方程:
(1)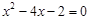
(2)8(3 -x)2 –72=0
如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(-5,0),且 ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.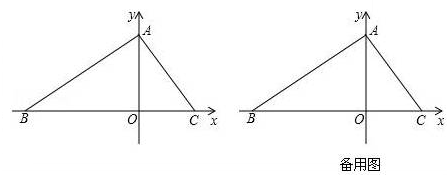
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出Q点坐标;若不存在,请说明理由.
杨佳明周日骑车从家里出发,去图书馆看书,
(1)若杨佳明骑车行驶的路程y(km)与时间t(min)的图象如图1所示,请说出线段AB所表示的实际意义: ;若杨佳明在第30分钟时以来时的速度原路返回,请在图上补出她返回时行驶的路程y(km)与时间t(min)的图象;
(2)在整个骑行过程中,若杨佳明离家的距离y(km)与时间t(min)的图象如图2所示,请说出线段AB所表示的实际意义: ;若杨佳明在第30分钟时以来时的速度原路返回,请在图上补出她返回时离家的距离y(km)与时间t(min)的图象;
(3)在整个骑行过程中,若杨佳明骑车的速度y(km/min)与时间t(min)的图象如图3所示,那么当她离家最远时,时间是在第 分钟,并求出她在骑行30分钟时的路程是 .
这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).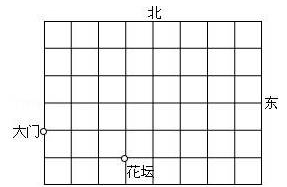
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.
在平面直角系中,已知A(-2,0),B(0,4),C(3,6);
(1)当D(6,0)时,求四边形ABCD的面积;
(2)在x轴上找一点P,使△PBC的周长最小,并求出此时△PBC的周长.