(桂林)如图,已知抛物线 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.

一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
| x |
3000 |
3200 |
3500 |
4000 |
| y |
100 |
96 |
90 |
80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
| 租出的车辆数 |
未租出的车辆数 |
||
| 租出每辆车的月收益 |
所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
问题背景:
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.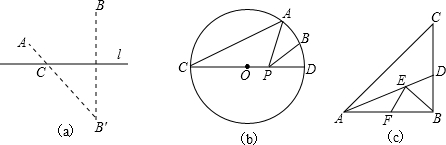
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为.
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
“端午”节前,小明爸爸去超市购买了大小、形状、重量等都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时从盒中随机取出火腿粽子的概率为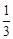 ;妈妈从盒中取出火腿粽子3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出火腿粽子的概率为
;妈妈从盒中取出火腿粽子3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出火腿粽子的概率为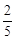 .
.
(1)请你用所学知识计算:爸爸买的火腿粽子和豆沙粽子各有多少只?
(2)若小明一次从盒内剩余粽子中任取2只,问恰有火腿粽子、豆沙粽子各1只的概率是多少?(用列表法或树状图计算)
如图,已知四边形ABDE是平行四边形,C为边B D延长线上一点,连结AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
(1)计算:  .
.
(2)已知,关于x的方程 的两个实数根
的两个实数根 、
、 满足
满足 ,求实数m的值.
,求实数m的值.