(内蒙古 呼 和 浩 特 )以下四个命题:
①若一个角的两边和另一个角的两边分别互相垂直,则这两个角互补.
②边数相等的两个正多边形一定相似.
③等腰三角形ABC中, D是底边BC上一点, E是一腰AC上的一点,若∠BAD=60°且AD=AE,则∠EDC=30°.
④任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
其中正确命题的序号为__________.
如图,已知线段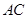 与
与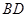 相交于点
相交于点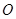 ,联结
,联结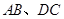 ,
,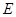 为
为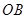 的中点,
的中点,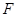 为
为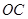 的中点,联结
的中点,联结 .若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.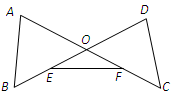
(本小题满分12分)阅读下列内容,设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三边长间的关系来判断这个三角形的形状:
①若 ,则该三角形是直角三角形;②若
,则该三角形是直角三角形;②若 ,则该三角形是钝角三角形;③
,则该三角形是钝角三角形;③ ,则该三角形是锐角三角形.
,则该三角形是锐角三角形.
例如一个三角形的三边长分别是4,5,6,则最长边是6,由于 ,故由上面③可知该三角形是锐角三角形,请解答以下问题:
,故由上面③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是三角形;
(2)若一个三角形的三条边长分别是3,4,x且这个三角形是直角三角形,则x的值为;
(3)若一个三角形的三条边长分别是 ,
, ,
, 请判断这个三角形的形状,并写出的判断过程.
请判断这个三角形的形状,并写出的判断过程.
(本小题满分10分)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)
(本小题满分10分)甲、乙两人分别从相距72千米的A,B两地同时出发,相向而行.甲从A地出发,走了2千米时,发现有物品遗忘在A地,便立即返回,取了物品后立即从A地向B地行进,结果甲、乙两人恰好在AB的中点处相遇.若甲每时比乙多走1千米,求甲、乙两人的速度.
解下列方程和方程组(每小题4分,共8分)
(1)
(2)