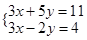(年贵州省黔东南州)去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
某蔬菜公司收购到某种蔬菜280吨,准备加工后上市销售.该公司的加工能力是:每天可以精加工12吨或者粗加工32吨.现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润为1500元,精加工后为3000元,那么该公司出售这些加工后的蔬菜共可获利多少元?
张老师带领该校七年级“三好学生”去开展夏令营活动,甲旅行社说:“如果老师买全票一张,则学生可享受半价优惠。”乙旅行社说:“包括老师在内按全票价的6折优惠。”若全票价为240元,当学生人数为多少人时,两家旅行社的收费一样多?
解方程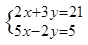
解方程