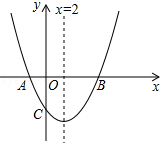
(年贵州省贵阳市)如图,经过点C(0,﹣4)的抛物线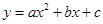 (
(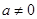 )与x轴相交于A(﹣2,0),B两点.
)与x轴相交于A(﹣2,0),B两点.
(1)a 0,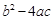 0(填“>”或“<”);
0(填“>”或“<”);
(2)若该抛物线关于直线x=2对称,求抛物线的函数表达式;
(3)在(2)的条件下,连接AC,E是抛物线上一动点,过点E作AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点E的坐标;若不存在,请说明理由.
若-3≤x≤2时,试化简│x-2│+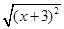 +
+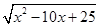 。
。
先化简,再求值.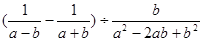 ,其中
,其中 ,
,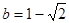
如图,已知矩形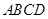 的边长
的边长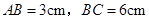 .某一时刻,动点
.某一时刻,动点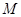 从
从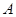 点出发沿
点出发沿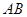 方向以
方向以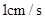 的速度向
的速度向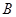 点匀速运动;同时,动点
点匀速运动;同时,动点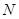 从
从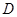 点出发沿
点出发沿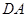 方向以
方向以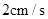 的速度向
的速度向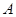 点匀速运动,设运动时间为t秒,问:
点匀速运动,设运动时间为t秒,问:
(1)用含t的代数式表示AN=___________cm;
(2)当t为何值时,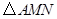 的面积等于矩形
的面积等于矩形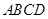 面积的
面积的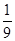 ?
?
(2)是否存在时刻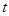 ,使以
,使以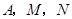 为顶点的三角形与
为顶点的三角形与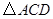 相似?若存在,求
相似?若存在,求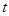 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.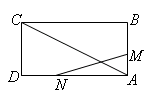
2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求A地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
已知关于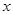 的一元二次方程
的一元二次方程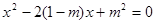 的两实数根为
的两实数根为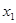 、
、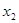 ;
;
(1)求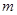 的取值范围;
的取值范围;
(2)设 ,当
,当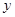 取得最小值时,求相应
取得最小值时,求相应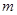 的值,并求出最小值。
的值,并求出最小值。