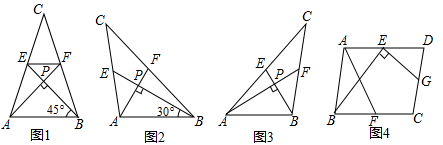
（年江西省南昌市）我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．
特例探索
（1）如图1，当∠ABE=45°，c=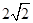
时，a= ，b= ．
如图2，当∠ABE=30°，c=4时，a= ，b= ．
归纳证明
（2）请你观察（1）中的计算结果，猜想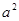
，
，
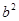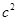三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．
拓展应用
（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=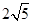
，AB=3，求AF的长．
DB，E是BC的中点，BE=
AC=2cm，求线段DE的长．
－1＝