如图所示,A球从倾角θ=30°的光滑斜面上某点由静止开始滚下,然后进入足够长的光滑水平面上,经M点时速度大小不发生变化,方向立刻变为水平向左.B球从M点开始向左做直线运动,g=10m/s2.
(1)若A球从斜面上某一高处静止滚下,同时B球以v0=8m/s向左做匀速直线运动,A球的高度满足什么条件,A、B两球能发生碰撞;
(2)若A球从斜面上N点静止开始滚下,MN=10m,B球同时从M点由静止向左以加速度a=2m/s2做匀加速直线运动,问:经多长时间两球相碰?
如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xOy平面向外.一电荷量为q、质量为m的带正电的运动粒子,经过y轴上y=b处的点P1时速率为v0,方向沿x轴正方向;然后,经过x轴上x=2b处的P2点进入磁场,并经过y轴上y=-2b处的P3点,不计粒子重力.求:
(1)电场强度的大小;
(2)粒子到达P2时速度的大小和方向;
(3)磁感应强度的大小.
如图所示,带负电的小球静止在水平放置的两平行金属板间,距下板h=0.8 m.两板间的电势差为300 V,如果两板间电势差减小到60 V,则带电小球运动到极板上需多长时间?(取g=10 m/s2)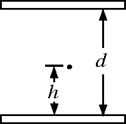
一台国产XQB30-13型全自动洗衣机说明书中所列的主要技术数据如下表。试根据表中提供的数据计算: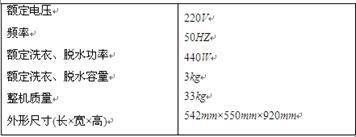
(1)这台洗衣机在额定电压下洗衣或脱水时,通过洗衣机的电流是多大?
(2)如洗衣、脱水的累计时间为40min,则洗衣机耗电多少度?
(3)若电机直流电阻为20欧,工作效率是多少?
一个带电粒子只在电场力作用下通过匀强电场中的a、b两点,一组平行的带箭头的实线表示匀强电场的电场线,如图所示。已知带电粒子通过a、b两点的速度大小分别是5 m/s和3 m/s,粒子的质量是100 g,a、b两点的电势差为80 V。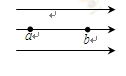
(1)试判断带电粒子所带电荷的种类。
(2)带电粒子所带的电荷量。
处于匀强磁场中的两根足够长、电阻不计的平行光滑金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接电阻或电容器.匀强磁场方向与导轨平面垂直,磁感应强度的大小B=2T,质量为0.02 kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触。若将下端连接阻值为R=20Ω的电阻,如图所示,(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)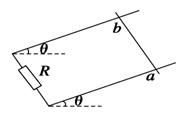
(1) 当金属棒下滑速度达到稳定时,求该速度的大小.
(2) 当金属棒下滑速度达到0.4m/s时,求加速度的大小.
(3) 若将下端连接的电阻换成电容为C=10000μF的电容器,求金属棒下滑的加速度.