下列命题：
①有一条直角边和斜边的高对应相等的两个直角三角形全等；
②有两边和其中一边上高对应相等的两个三角形全等；
③有两边和第三边上的中线对应相等的两个三角形全等；
④有两边和其中一边上的中线对应相等的两个三角形全等．
其中正确的命题有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
在下面方程中变形正确的为（）．
①3x+6=0，变形为x+2=0，②x+7=5-3x，变形为4x=-2，③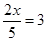
，变形为2x=15，④4x=-2，变形为x=-2．
| A．①③ | B．①②③ | C．③④ | D．①②④ |
下列方程是一元一次方程的是（）．
A． |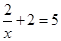
B． |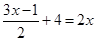
C． |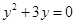
D．9x-y=2 |
下列说法中正确的个数为（）．
①在同一平面内不相交的两条直线叫做平行线，
②平面内经过一点有且只有一条直线与已知直线垂直，
③经过一点有且只有一条直线与已知直线平行，
④平行同一直线的两直线平行．
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，与OH相等的线段有（）．
| A．8 | B．7 | C．6 | D．4 |
在同一平面内，三条直线的交点个数不能是（）．
| A．1个 | B．2个 | C．3个 | D．4个 |