(本小题满分12分)已知函数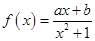 在点
在点 处的切线方程为
处的切线方程为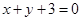 .
.
(1)求函数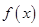 的解析式;
的解析式;
(2)设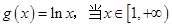 时,求证:
时,求证: ;
;
(3)已知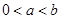 ,求证:
,求证: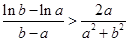 .
.
(本小题满分14分)
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
(本小题满分10分)
已知 .
.
⑴求 及
及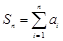 ;
;
⑵试比较 与
与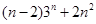 的大小,并说明理由.
的大小,并说明理由.
(本小题满分10分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 。现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止。若摸出白球,则记2分,若摸出黑球,则记1分。每个球在每一次被取出的机会是等可能的。用x表示甲,乙最终得分差的绝对值.
。现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止。若摸出白球,则记2分,若摸出黑球,则记1分。每个球在每一次被取出的机会是等可能的。用x表示甲,乙最终得分差的绝对值.
(1)求袋中原有白球的个数;
(2)求随机变量x的概率分布列及期望Ex.
选修4-5:不等式选讲)已知x,yR,且|x+y|≤,|x-y|≤,求证:|5x+y|≤1.
选修4-4:坐标系与参数方程)已知极坐标系的极点与直角坐标系的原点重合,极轴与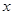 轴的正半轴重合.若直线
轴的正半轴重合.若直线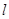 的极坐标方程为
的极坐标方程为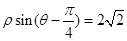 .
.
(1)把直线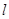 的极坐标方程化为直角坐标系方程;
的极坐标方程化为直角坐标系方程;
(2)已知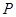 为椭圆
为椭圆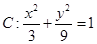 上一点,求
上一点,求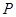 到直线
到直线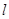 的距离的最小值.
的距离的最小值.