如图,动点 在正方体
在正方体 的对角线
的对角线 上,过点
上,过点 作垂直于平面
作垂直于平面 的直线,与正方体表面相交于
的直线,与正方体表面相交于 ,
, ,设
,设 ,
, ,则函数
,则函数 的图像大致是( )
的图像大致是( )


已知函数 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 的解析式是()
的解析式是()
A. |
B. |
C. |
D. |
设 ,则a, b,c的大小关系是( )
,则a, b,c的大小关系是( )
| A.b>c>a | B.a>b>c | C.c>a>b | D.a>c>b |
设 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( )
A. |
B. |
C. |
D. |
命题“存在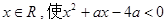 ”为假命题是命题“
”为假命题是命题“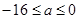 ”的( )
”的( )
| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
下列推理是归纳推理的是 ()
A.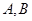 为定点,动点 为定点,动点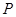 满足 满足 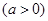 ,则动点 ,则动点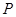 的轨迹 的轨迹是以 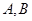 为焦点的双曲线; 为焦点的双曲线; |
B.由 求出 求出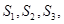 猜想出数列 猜想出数列 的前 的前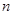 项和 项和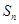 的表达式; 的表达式; |
C.由圆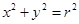 的面积 的面积 ,猜想出椭圆 ,猜想出椭圆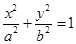 的面积 的面积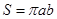 ; ; |
| D.科学家利用鱼的沉浮原理制造潜水艇. |