(本小题满分14分)
设函数 .
.
(1)若函数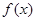 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数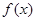 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
(本小题满分12分)在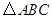 中,内角
中,内角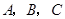 对边的边长分别是
对边的边长分别是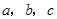 ,已知
,已知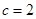 ,
,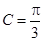 .
.
(1)若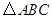 的面积等于
的面积等于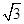 ,求
,求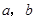 ;
;
(2)若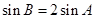 ,求
,求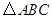 的面积.
的面积.
如图,轴截面为边长是2的正方形的圆柱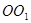 内有一个三棱柱
内有一个三棱柱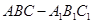 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆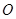 的直径.
的直径.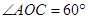
(1)求三棱柱 的体积;
的体积;
(2)证明:平面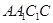 ⊥平面
⊥平面

等差数列 的前
的前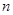 项和记为
项和记为 ,已知
,已知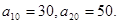
(1)求通项 ;
;
(2)若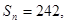 求
求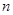 。
。
本题满分12分)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c, a=2bsinA
(1)求B的大小;
(2)求cosA+sinC的取值范围.
已知奇函数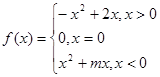 ;
;
(1)求实数m的值,并在给出的直角坐标系中画出 的图象;
的图象;
(2)若函数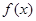 在区间[-1,|
在区间[-1,| |-2]上单调递增,试确定
|-2]上单调递增,试确定 的取值范围.
的取值范围.