公元前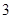 世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(
世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(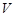 )与它的直径(
)与它的直径( )的立方成正比”,此即
)的立方成正比”,此即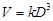 ,欧几里得未给出
,欧几里得未给出 的值.
的值.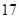 世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式
世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式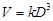 中的常数
中的常数 称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式
称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式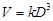 求体积(在等边圆柱中,
求体积(在等边圆柱中,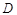 表示底面圆的直径;在正方体中,
表示底面圆的直径;在正方体中,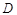 表示棱长).假设运用此体积公式求得球(直径为
表示棱长).假设运用此体积公式求得球(直径为 )、等边圆柱(底面圆的直径为
)、等边圆柱(底面圆的直径为 )、正方体(棱长为
)、正方体(棱长为 )的“玉积率”分别为
)的“玉积率”分别为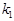 、
、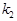 、
、 ,那么
,那么 ( )
( )
A. |
B.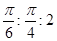 |
C.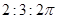 |
D.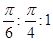 |